Tricks of the Trade

The Usual Way Is Just Fine, Man.

Posted by

2

Tricks of the Trade

(with Professor Glesser)

As I mentioned in this much-maligned post, “my all-time favorite differentiation technique is logarithmic differentiation.” In that post, I give examples of two types of problems where the technique proves useful. The second type—where a variable function is raised to a variable power—is handled with the SPEC rule (essentially the sum of the power rule and exponential rule, with the chain rule used as per normal). Here is the example I gave of a function of the first type.
y = \sqrt[3]{\dfrac{(3x-2)^2\sqrt{2x^3+1}}{x^4(x-1)}}
Typically, I show the students how to use logarithmic differentiation in order to compute the derivative of this type of function (see the post linked to above for the full derivation). However, this is not how I compute it myself!


Story Time

Like most everybody who takes calculus, I learned the quotient rule for differentiation:

\left(\dfrac{f}{g}\right)' = \dfrac{g \cdot f' - f \cdot g'}{g^2}

Or, in song form (sung to the tune of Old McDonald):

Low d-high less high d-low
E-I-E-I-O
And on the bottom, the square of low
E-I-E-I-O
[Note that when sung incorrectly as High d-low less low d-high, the rhyme will not work!]

At some point, I was given an exercise to show that
\left(\dfrac{f}{g}\right)' = \dfrac{f}{g}\left(\dfrac{f}{f'} - \dfrac{g}{g'}\right).
If you start from this reformulation, it is a simple matter of algebra to get to the usual formulation of the quotient rule. However, a couple of things caught my eye. First, the reformulation seemed much easier to remember: copy the function and then write down the derivative of each function over the function and subtract them; the order is the “natural” one where the numerator comes first.

Story Within A Story Time

Actually, there is a reasonably nice way to remember the order of the quotient rule, at least if you understand the meaning of the derivative. Assume that both the numerator and denominator are positive functions. If the derivative of the numerator is increasing, then the numerator and the quotient are getting bigger faster, so the derivative of the quotient should also be getting bigger, i.e., f' should have a positive sign in front of it. Similarly, if the derivative of the denominator is increasing, then the denominator is getting bigger faster, which means the quotient is getting smaller faster, and so the derivative of the quotient is decreasing, i.e., g' should have a negative sign in front of it.

Secondly, the appearance of the original function in the answer screams: LOGARITHMIC DIFFERENTIATION. Let’s see why.

If y = \dfrac{f}{g}, then \ln(y) = \ln\left(\dfrac{f}{g}\right) = \ln(f) - \ln(g). Differentiating both sides using the chain rule yields
\dfrac{y'}{y} = \dfrac{f'}{f} - \dfrac{g'}{g},
and so the result follows by multiplying both sides by y. This is one of my favorite exercises to give first year calculus students—before and after teaching them logarithmic differentiation*.

*Don’t you think that giving out the same problem at different times during the course is an underutilized tactic?

Being a good math nerd, I had to take this further. What if the numerator and denominator are, themselves, a product of functions? Assume that f = f_1 \cdot f_2 \cdots f_m and that g = g_1 \cdot g_2 \cdots g_n. Setting y = \dfrac{f}{g}, taking the natural logarithm of both sides, and applying log rules, we get:

\ln(y) =\ln(f_1) + \ln(f_2) + \cdots + \ln(f_m) -\ln(g_1) - \ln(g_2) - \cdots - \ln(g_n).

Differentiating (using the chain rule, as usual) gives:

\dfrac{y'}{y} = \dfrac{f'_1}{f_1} + \dfrac{f'_2}{f_2} + \cdots + \dfrac{f'_m}{f_m} - \dfrac{g'_1}{g_1} - \dfrac{g'_2}{g_2} - \cdots - \dfrac{g'_n}{g_n}.

Multiplying both sides by y now gives us the formula:

y' = \dfrac{f}{g}\left(\dfrac{f'_1}{f_1} + \dfrac{f'_2}{f_2} + \cdots + \dfrac{f'_m}{f_m} - \dfrac{g'_1}{g_1} - \dfrac{g'_2}{g_2} - \cdots -\dfrac{g'_n}{g_n}\right).

An immediate example of using this is as follows. Differentiate y = \dfrac{\sin(x)e^x}{(x+2)\ln(x)}. The usual way would involve the quotient rule mixed with two applications of the product rule. The alternative is to simply rewrite the function, and to work term by term giving:

y' = \dfrac{\sin(x)e^x}{(x+2)\ln(x)}\left(\dfrac{\cos(x)}{\sin(x)} + \dfrac{e^x}{e^x} - \dfrac{1}{x+2} - \dfrac{1/x}{\ln(x)}\right),

which immediately reveals some rather easy simplifications.

But we haven’t used all of the log rules yet! We haven’t used the exponential law. So, let’s assume that each of our f_i's and g_j's has an exponent, call them a_i and b_j, respectively. In this case, using logarithmic differentiation, we get:

\ln(y) = a_1\ln(f_1) + \cdots + a_m\ln(f_m) - b_1\ln(g_1) - \cdots - b_n\ln(g_n).

Differentiating, we get almost the same formula as above, but with some extra coefficients:

y' = \dfrac{f}{g}\left(a_1\dfrac{f'_1}{f_1} + \cdots + a_m\dfrac{f'_m}{f_m} - b_1\dfrac{g'_1}{g_1} - \cdots - b_n\dfrac{g'_n}{g_n} \right).

Look back to the example near the top of the post. If we rewrite it with exponents instead of roots, we get:

y = \dfrac{(3x-2)^{2/3}(2x^3 + 1)^{1/6}}{x^{4/3}(x-1)^{1/3}}.

Taking the derivative is now completely straight-forward.

y' = \dfrac{(3x-2)^{2/3}(2x^3 + 1)^{1/6}}{x^{4/3}(x-1)^{1/3}}\left(\dfrac{2}{3}\cdot\dfrac{3}{3x-2} + \dfrac{1}{6}\cdot\dfrac{6x^2}{2x^3+1} - \dfrac{4}{3}\cdot\dfrac{1}{x} - \dfrac{1}{3}\cdot \dfrac{1}{x-1}\right).

Again, there is some simplifying to be done.

An easier problem is one without a denominator! Let y = \tan(2x)x^{3/4}(3x-1)^3. Normally, one would use the product rule here, but why don’t we try our formula. It gives:

y' = \tan(2x)x^{3/4}(3x-1)^3\left(\dfrac{2\sec^2(2x)}{\tan(2x)} + \dfrac{3}{4}\cdot \dfrac{1}{x} + 3\dfrac{3}{3x-1}\right).

That was pretty painless, while the product rule becomes more tedious as the number of factors in the product increases.

Oh, and if you can’t imagine this being appropriate to teach to students, no less an authority than Richard Feynman encouraged his students to differentiate this way. At the very least, his support gives me the confidence to let you in on my little secret.

In Defense of Shrtcts

Posted by

0

Several times, I have written about handy shortcuts that bypass some of the tedium of calculation.The frequency with which readers derided these tricks or mnemonics surprised me. For instance, my post on a shortcut for logarithmic differentiation ended up being the topic of a Facebook debate on sound pedagogy. One of the participants claimed that he would never teach the SPEC rule since he would rather the students know how to use logarithmic differentiation. It seemed to me that this is equivalent to not teaching the power rule because you would rather the students know how to evaluate limits and to utilize the binomial theorem.

Let’s face it, anyone who disagrees with using shortcuts or mnemonics probably should add, “at least in addition to the shortcuts and mnemonics that are already in common use.” Our entire system of notation is designed (sometimes poorly) to make the meaning easier to remember and computations easier to perform, e.g., decimal notation versus Roman numerals. There is nothing wrong with observing that a long computation reveals a pattern or an invariant that allows for a more direct route to the answer; this is a process embraced by mathematicians (I’d love to know what percentage of math papers simply improve on the proof of a known result).

Am I wrong or is there a misconception that teaching a shortcut implies not teaching the reason behind the shortcut? When I was in ninth grade, I did a project on mental arithmetic. The teacher gave back my draft with a comment asking for justifications of the tricks I was using. I learned so much about algebra trying to complete that assignment, perhaps more than I would learn in an entire high school algebra course. Make learning the inner-workings a priority, and the shortcuts arise naturally.

The June 2012 issue of the Notices of the AMS contains a provocative article by Frank Quinn. Amongst other things, he stresses that work on an abstract and symbolic level is important. Of course, there are lots of ways of incorporating abstraction into a class. Wouldn’t it be doubly beneficial if the result of that work was a faster way to perform a calculation?

Integration by Parts 3

Posted by

0

Tricks of the Trade

(with Professor Glesser)

In the first two installments of this series

Integration by Parts 1
Integration by Parts 2

we introduced integration by parts as a way to compute antiderivatives of a product of functions and we saw how certain integration by parts problems are handled more efficiently with the so-called tabular method (or, in Stand and Deliver, the “tic-tac-toe” method). In this post, we will consider the following question: As integration by parts requires the making of a choice—which is your u and which is your dv—how can we make this choice so that the resulting integral is easier to compute?

From the Mailbag

Über-reader CalcDave wrote in the comments to the last post in this series that,

I usually make a show of how sometimes the order does matter…That is, I’ll let u = x^4 and dv = \sin(x)\ dx the first time and then go through it and say something like, “Well, that didn’t get us much of anywhere. What if we switch up our u and dv this time? Let’s let u = \cos(x) and dv = x^3.” Then when you work it through, everything cancels out and we’re back to the original problem.

Indeed, Dave. Let’s take a look at what happens if we switch it up.

Egad, Dave is right. Since the product of the terms in the last line of the table is what we will need to integrate, doing it this way just makes things worse.  Ah, but what if we start with the cosine on the left and then switch it up? Oh, yeah, we’ll just get back what we started with. This suggests that we should always put a polynomials on the left so that it doesn’t go up in degree. It turns out that there are several examples where this is precisely the wrong thing to do. We implicitly saw this in the first post, but let me give you a couple of more explicit examples.

\int x\sin^{-1}(x)\ dx

If we split this up using our ‘rule’ to always put the polynomial on the left, then we are forced to integrate \sin^{-1}(x). Let’s say you just happen to know the antiderivative of \sin^{-1}(x) is x\sin^{-1}(x) + \sqrt{1 - x^2} + C (I didn’t, although I can use integration by parts to figure it out!). You would now get:
and be forced to integrate the monstrosity on the right. Not for me thank you. However, if you put the \sin^{-1}(x) on the left, we get:
and at the very least we have gotten rid of the \sin^{-1}(x). In fact we have done more, but we’ll have to wait until the next post to resolve this.

Another example is \int x\ln(x)\ dx. Although we did integrate \ln(x) in our first post, it gave an answer of x\ln(x) - x + C and we don’t want to integrate that since it we don’t know how to integrate x\ln(x) (in a future post, we will resolve this last problem directly). On the other hand, if we put the \ln(x) on the left, the derivative will return \frac{1}{x} and the natural logarithm is gone. So when does it pay to put the polynomial on the right? Whenever the derivative of the other function changes it into an algebraic function, it will be right to integrate the polynomial. Otherwise, you should differentiate the polynomial. If we also include trigonometric functions and exponential functions, the rule of thumb is:
Logarithms Inverse-Trig Algebraic Trig Exponential

This list represents a good order in which to choose your u in the following sense: if you have two functions, whichever comes first in the above list should be your u. Some people enjoy a good mnemonic to memorize the order. I’ve heard the following:

LIATE rule (or alL I ATE rule)

Lions In Africa Tackle Elephants

Liberals In America Typify Elitists

Little Indians Are Tiny Engines

Lets Integrate All The Equations

This says, for example, that when confronted with \int \sin(x) e^x\ dx, differentiate the \sin(x) and integrate e^x.

Next Time

In our next segment, we will introduce the box method for handling several of the integrals left unsolved in this post.


Integration by Parts 2

Posted by

3

Last time on

Tricks of the Trade

(with Professor Glesser)

we introduced integration by parts as an analogue to the product rule. We start this post with an example to show why the method can become tedious.

Consider

\int x^4\sin(x)\ dx

As there is a product of functions, this seems ideal for integration by parts. A question we will take up in our next post is which term we should look to differentiate (i.e., be our u) and which we should antidifferentiate (i.e., be our dv). For now, I will give you that a sound choice is

u = x^4 \qquad dv = \sin(x)\ dx

With this, we get

du = 4x^3\ dx \qquad v = -\cos(x).

Using the integration by parts fomula:

\int u\ dv = uv - \int v\ du

we get

\int x^4\sin(x)\ dx =-x^4\cos(x)-\int 4x^3(-\cos(x))\ dx

Using linearity, we reduce the question to solving \int x^3\cos(x)\ dx.

Hold on, now. Is that really an improvement?

Yes, because the power of x is smaller. But, I’ll grant you that life doesn’t seem much better. Essentially, we need to do integration by parts again. So, we rename things:

u = x^3 \qquad dv = \cos(x)\ dx
du = 3x^2\ dx \qquad v = \sin(x)

and we get

\int x^3\cos(x)\ dx = x^3\sin(x) - \int 3x^2\sin(x)\ dx

and after using linearity, we only need to compute \int x^2\sin(x).

Check please!

Before you get up and leave, notice that the power of x is one less again.

Whoo-hoo. Yay, capitalism!

Seriously, each time we do this process, the exponent will decrease by one (since we are differentiating). So we “only” need to do it two more times.

You suck, Professor Glesser

Agreed. This is why it is nice to automate the process. I first learned this by watching Stand and Deliver over and over while in high school. I am not much of a fan of Battlestar Galactica (nerd cred…plummeting) and the few times I watched, I thought Edward James Olmos’ portrayal of William Adama was really flat; I thought Olmos was mailing in the performance. The most likely reason for my feelings? If you’ve never seen it, watch Stand and Deliver and Olmos’ portrayal of math teacher Jaime Escalante. Now that was a performance. Anyhow, here is the clip I watched incessantly.

I decided on a different notational scheme, but the method is the same. We make the following observation: when doing integration by parts repeatedly, the term that we differentiate will usually be differentiated again. That is, (abusing notation) the du becomes our new u. If you like, the formula for integration by parts has us multiply diagonally left to right (uv) and then subtract the integral of the product left to right along the bottom (-\int v\ du):

The next iteration of integration by parts gives:

Essentially, this creates an alternating sum. In practice, it means we can set up the following chart where, going down, we differentiate on the left until we get 0 and antidifferentiate on the right as many times as we differentiated.

Notice here that we are condensing quite a bit of notation with this method since we are no longer using the u, v, du, and dv notation. But, we are getting out precisely the same information. We draw diagonal left-to-right arrows to indicate which terms multiply and we superscript the arrows with alternating pluses and minuses to give the appropriate sign.

We don’t need to draw a horizontal arrow on the bottom since that would simply give us the antiderivative of 0 \cdot (-\cos(x)) = 0. Following the arrows and taking account of signs, our antiderivative is

-x^4\cos(x) + 4x^3\sin(x)+ 12x^2\cos(x)- 24x\sin(x)- 24\cos(x)+C

Could you do that again?

Let’s try a different example, a little more complicated. Say we want to compute \int (2x^2- 3x + 4)\cos(3x)\ dx. We simply set up the chart where, going down, we differentiate on the left and antidifferentiate on the right:

and follows the arrows to get

\frac{1}{3}(2x^2 - 3x+4)\sin(3x)+ \frac{1}{9}(4x-3)\cos(3x)- \frac{4}{27}\sin(3x)+C
as the antiderivative for \int (2x^2- 3x + 4)\cos(3x)\ dx.

I think I need a break

Indeed. Next time we’ll take this a step further and show how to handle some situations where neither function is a polynomial. This will also bring up the question, again, about how to choose which function to differentiate and which to integrate.

Integration By Parts 1

Posted by

4

This is the first in a series of posts on one of my favorite methods of antidifferentiation: integration by parts. I didn’t love it at first, but a little practice and a few tricks made me appreciate it. Teaching it, well, that is where the love affair begins.

Tricks of the Trade

(with Professor Glesser)

What are you talking about?

Let me assume that the reader is familiar with basic differentiation (including the product rule) and antidifferentiation of some basic elementary functions, i.e., the reader knows such facts as the power rule and how to antidifferentiate exponential functions as well as sine and cosine.

Integration by parts is an analogue to the product rule for derivatives (which tells you how to differentiate a product of functions). In the language of differentials, we have

d(uv) = u\ dv + v\ du

for functions u and v of some common variable, say x. Integrating both sides, we get

uv = \int d(uv) = \int u\ dv + \int v\ du.

The usual form of the integration by parts formula is now obtained by subtracting a term:

\int u\ dv = uv - \int v\ du.

Uh…What?

An example may be helpful. A canonical first example is \int x\sin(x)\ dx. The typical calculus student, fooled by the simplicity of the sum rule and not having the product rule in mind, will incorrectly assert \int x \sin(x)\ dx = (\int x\ dx)(\int \sin(x)\ dx) = (\frac{1}{2}x^2)(-\cos(x)) = -\frac{1}{2}x^2\cos(x). Of course, differentiating shows that this answer is wrong. Why? Well, because antidifferentiation is additive but isn’t multiplicative.

So let’s try the integration by parts formula. We start by noting that \sin(x) is the derivative of -\cos(x), i.e., d(-\cos(x)) = \sin(x)\ dx. Consequently, we could write

\int x \sin(x)\ dx = \int x\ d(-\cos(x)).

We may now apply the integration by parts formula where u = x and v = -\cos(x). This gives

\int x\ d(-\cos(x)) = -x\cos(x) - \int -\cos(x)\ dx = -x\cos(x) + \sin(x) + C.

Could I see one more?

Sure, here is a less obvious example. Consider \int \ln(x)\ dx.

Wait, there is no product of functions.

There is a product; it is just a bit silly. You see \ln(x) = \ln(x)\times 1. Yes, it is one of those kinds of tricks. Now, I know that 1 is the derivative of x and so I can use the integration by parts formula with u = \ln(x) and v = x. This gives:

\int \ln(x)\ dx = x\ln(x) - \int x\ d(\ln(x)) = x \ln(x) - \int x \frac{1}{x}\ dx = x\ln(x) - \int dx = x\ln(x) - x + C.

How do I keep everything straight?

A very common bookkeeping measure is to make a little table including u, v, du and dv. For our first example, you would start with:

u = x \qquad dv = \sin(x)\ dx
du = ? \qquad v = ?

You then compute du = 1\ dx = dx and v = -\cos(x) to complete the table:

u = x \qquad dv = \sin(x)\ dx
du = dx \qquad v = -\cos(x)

You can then simply plug everything into the integration by parts formula.

This isn’t so bad. Why do you need multiple posts?

For those who don’t know the punchline, I won’t spoil it here. It suffices to say that there are some harder problems out there and there are some really efficient ways of handling these difficulties. Stay tuned!

The Circle Is Now Complete

Posted by

7

Tricks of the Trade

(with Professor Glesser)

I watched a very nice video on remembering the values of sine and cosine at the various standard angles 0, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{\pi}{2} (or, in degrees, 0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}, 90^{\circ}) and their second through fourth quadrant analogues. My method is only slightly different and is likely well-known, but as most of my students have never seen it, I figure there is at least one person out there I can help. This also gives me an opportunity to throw out a useful mnemonic that naturally attaches itself to the unit circle.

Get your students fingering with each other!

The first step is for your students to be absolutely, 100% comfortable with the standard angles mentioned above. I will assume that this is done. Hold up your hand (either will work) with your palms facing either away or toward you, and starting from the leftmost finger, count 0, 30, 45, 60, 90 or 0, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{\pi}{2}.

You don’t need to remember which value goes with which finger; you only need to be able to recite the list and stop at the correct finger. When you get to the desired angle, put the corresponding finger down. Now flip your hand over. We will use the number of fingers on the left of the bent finger to determine the cosine of the angle and the number of fingers on the right to compute the sine of the angle. The formula for the value is “ROOT FINGERS OVER 2”

For example, to compute the cosine and sine of \frac{\pi}{6}, starting with my palm facing in, I put down the second finger from the left and flip over my hand:

The number of fingers on the left of the bent finger gives you the cosine, the fingers on the right give you the sine. Just remember ROOT FINGERS OVER 2. Why the hand flip?

Truthfully, I never used it. However, I added it because I wanted to reinforce the fact that when you define cosine and sine via the unit circle (as I do), then the coordinates on the unit circle are of the form (\cos(\alpha), \sin(\alpha)).
To make this consistent with the hand trick, you need to flip the hand.

What was this mnemonic you mentioned?

It is actually pretty silly. The following (ridiculous) diagram should help a student remember where sine and cosine are positive and negative. They need only remember where the S goes and where the C goes. “S stands for summit, so it goes on the top” has worked for my students.

Furthermore, this diagram, when read clockwise, gives you derivatives of sine and cosine (as well as their negatives). That is not too shabby.

Stupid Factoring Trick

Posted by

4

After the up tick in hits from my last post, WordPress asked if I’d post something to decrease the load on their servers and so I bring to you the fourth installment of my widely panned series on mathematical shortcuts. Today’s topic:  Factoring.

Tricks of the Trade

(with Professor Glesser)

Quick: what do the following polynomials have in common?

5x^2 - 6x + 1

-3x^2 + 13x - 10

x^3 - 4x^2 + 2x + 1

If you said, in less than 10 seconds, that 1 is a root to all of them, you can probably stop reading now! I did it in less than 3 seconds, so I should stop reading, but given that I’m writing this, that would be problematic.

The trick isn’t really a trick. It is just plain obvious once you see it. If you plug x=1 into any of the polynomials, you are left with 0, so it is a root. But, if that is what you do, then you won’t see the trick. When you plug 1 in, the x parts simply vanish and you are left adding up the coefficients. For example, if you notice that 5 – 6 + 1 = 0, then you know immediately that 1 is a root. In fact, that is how I came up with all the examples: I made up all but the last coefficient psuedo-randomly and then made the last coefficient the opposite of the sum of the other coefficients!

Is that it?

No, there’s more. Already, we know that 5x^2 - 6x + 1 has x = 1 as a root, but we can also immediately find the other root. How? Let’s factor. Since 1 is a root, we know that x-1 is a divisor of 5x^2 -6x + 1 and so 5x^2 -6x +1 = (x-1)(px+q) = px^2 + (p-q)x - q. Equating coefficients, we get p = 5 and q = -1. In other words, the other root is -q/p = 1/5. Hmmm, that wasn’t so immediate; that took effort. Fine, lets start over with an arbitrary quadratic ax^2 + bx + c such that a + b + c = 0 (implying that 1 is a root). We can factor ax^2 + bx + c = (x-1)(px + q) = px^2 + (q-p)x - q and, equating coefficients, we get p = a and c = -q. Ah, hah! So under our assumptions, the roots are 1 and c/a.

If we go back to our second example from the beginning, we can now immediately see that the roots are 1 and \dfrac{-10}{-3} = \dfrac{10}{3}.

Pretty good. That it?

No way. If you start with a cubic whose coefficients sum to 0, then we can factor it as before:

ax^3 + bx^2 + cx + d = (x-1)(px^2 + qx + r) = px^3 + (q-p)x^2 + (r-q)x -r

from which we get p = a, r = -d and q = \dfrac{a+b-c-d}{2} (that last one takes more work than the others). This isn’t quite as nice as before (not even close, actually), but if you’re into obscure formulas, this might be your cup of tea.  Let me give another example of a cubic, though, that is a little more fun.

Consider 3x^3 - 8x^2 + 7x - 2. At this point, your x = 1 root detector should be screaming like my two-year old when he spots a caterpillar on the ground. But, if you quickly compute a - d + \dfrac{1}{2}(a+b-c-d), you also get 0. Meaning that x = 1 is a double root (i.e., (x-1)^2 divides 3x^3 - 8x^2 + 7x - 2). It also means that the third root is 3/2!

I know, I know: there’s more.

That’s right, Diane. Part of the reason this trick will work so often in math class is that textbook writers are lazy. Why make up problems with realistic roots when you can make them all have the same roots? Anecdotally, the three most common roots of polynomials in textbooks are 0,1,-1. Checking for 0 as a root is pretty straightforward and I’ve just shown you how to find 1 as a root; how about -1? It is only slightly more complicated.

Let’s start with our general quadratic again: ax^2 + bx + c. If we substitute -1 in for x, every even power of x will simply vanish, while the odd powers of x will negate the sign of the coefficient. That is, you get a - b + c. If this equals 0, then -1 is a root. For example, knowing that 4 - 7 + 3 = 0 implies that -1 is a root of 4x^2 + 7x + 3. As before, we can factor: ax^2 + bx + c = (x+1)(px + q) = px^2 +(q+p)x + q and so p =a and q = c. Thus, the other root is -c/a. This tells us that the other root of 4x^2 + 7x + 3 is -3/4.

As before, there is no reason to stop at quadratics. For a general cubic ax^3 + bx^2 + cx + d, you simply check whether -a +b -c + d = 0.

Put together, you now have a really good way to spot check whether the three most common (textbook) roots occur in a given polynomial.

Phew, we’re done.

Not quite. I have one last bit for the interested. My high school algebra teacher taught us the rational root test (do they still teach this in school?) which says that the rational roots of a polynomial of degree n (rational here means an integer divided by a non-zero integer and the degree of a polynomial is the highest power of x in the polynomial) of the form ax^n + \cdots + b (where I don’t care at all about the terms in the middle) are all of the form \dfrac{p}{q} where p divides b and q divides a. In the special case where a,b \in \{\pm 1\}, then there are only two possible rational roots: 1 and -1. So, if given

x^5 + 2x^4 - 5x^3 + 2x^2 + 4x - 1

we can immediately see by adding the coefficients that 1 is not a root and by negating the odd power coefficients and adding that -1 is not a root and so, by the rational root test, this quintic polynomial is irreducible (i.e., it can’t be factored¹).

For another cool factoring trick that I don’t use (because I only just learned it), but think I might try teaching is David Cox’s Bottom’s Up! method.

¹This means “can’t be factored over the rationals” which means that you can’t factor so that the coefficients of the factors are rational numbers. The polynomial x^2 - 5 can be factored as (x + \sqrt{5})(x-\sqrt{5}), but \pm \sqrt{5} are irrational numbers.

A symmetry trick for integration

Posted by

0

Tricks of the Trade

(with Professor Glesser)

Parentheses in mathematics never fails to impress me. Take, for instance, the freshman dream:

(x + y)^2 = x^2 + y^2

FAIL!

Not only do the parentheses matter, but in nontrivial way. Another of my favorite examples is the difference between \sin(x)^2 and \sin(x^2). Just a teeny little difference that makes all the difference in the world. You see, the first function is always greater than or equal to 0. Here are their graphs:

\mathbf{\sin(x)^2}

\mathbf{\sin(x^2)}

Outside of (-2,2), they aren’t even close. Of course, this suggests that if you integrate them, you expect to get wildly different answers (there are some exceptions to this: try integrating both from 0 to \pi/4). Ah, but there is a little problem when you try to integrate, isn’t there? You can probably handle (possibly with a great deal of effort) finding an antiderivative for \sin(x)^2, but more about that in a bit. Rather oddly, there is no elementary antiderivative for  \sin(x^2). Integrating it from 0 to x gives an example of a Fresnel integral, but already this is beyond what most of my students want to hear in calculus. So, let’s talk about what we can actually do.

C’mon, Get to the Trick

I’ve seen two reasonable ways to find the antiderivative of \sin(x)^2 = \sin^2(x): integration by parts and trig identities. The former method is actually used twice along with a little trick (I’ll get back to this later in the summer when I have a four-part series on integration by parts), while the latter requires you to remember how to convert products of sines into the cosine of a sum. I tend to use the former since I don’t have to remember anything, but the latter is probably a bit easier.

Using either method, we get \sin^2(x) = -\dfrac{1}{2} \sin x \cos x + \dfrac{x}{2} + C. Now, say that we want to compute \displaystyle\int_0^{2\pi} \sin^2(x)\ dx (this is a rather common integral that seems to show up quite a bit in integral calculus and, especially, in multivariable calculus when you start doing coordinate changes). Using the fundamental theorem of calculus, we have:

\displaystyle\int_0^{2\pi} \sin^2(x)\ dx = -\dfrac{1}{2} \sin x \cos x + \dfrac{x}{2} \bigg\vert^{2\pi}_0

= \left(-\dfrac{1}{2}\sin(2\pi)\cos(2\pi) + \dfrac{2\pi}{2}\right) - \left(-\dfrac{1}{2}\sin(0)\cos(0) + \dfrac{0}{2}\right)

and after realizing all the terms but one are 0, we see that the integral evaluates as \pi.

Some trick. I already knew how to do that.

Here is the trick. Notice that \sin(x) and \cos(x) have nearly identical graphs on [0, 2\pi], the only difference is a shift. This implies that if you integrate them on [0, 2\pi], you should get the same answer, i.e., \displaystyle\int_0^{2\pi} \sin(x)\ dx =\displaystyle\int_0^{2\pi} \cos(x)\ dx. If we square both functions, the same result holds: \displaystyle\int_0^{2\pi} \sin^2(x)\ dx = \displaystyle\int_0^{2\pi} \cos^2(x)\ dx ( you better convince yourself of this before moving on).

From here, we get \displaystyle\int_0^{2\pi} \sin^2(x)\ dx = \dfrac{1}{2}\displaystyle\int_0^{2\pi} \sin^2(x) + \cos^2(x)\ dx.

Why did we clutter up our integrand? Because, of course, we didn’t. The integrand is 1 and hence the integral evaluates to the length of the interval. In particular, \displaystyle\int_0^{2\pi} \sin^2(x)\ dx =\dfrac{1}{2}(2\pi) = \pi.

Cool, no?

But that is just one integral

True, but it is an important one. False, because obviously we can use it to compute \displaystyle\int_0^{2\pi} \cos^2(x)\ dx = \pi. Okay, that is cheating a bit. But we can actually go a little further. First, we really didn’t think hard enough about the last example. Consider the graph of \sin^2(x) on [0, \pi]:

Notice that we get a full period of \sin^2(x). Therefore, the reason what we did above worked on [0, 2\pi] is that it works on [0, \pi] and we just repeated it.  Instead of the observation about \cos^2(x) , we could also draw a rectangle with height 1 and width \pi and remark that the area under the graph makes up precisely half the area of the rectangle, i.e., \displaystyle\int_0^{\pi} \sin^2(x)\ dx = \dfrac{1}{2}(\pi) = \dfrac{\pi}{2}. The graph makes it obvious that we could also look at only [0, \pi/2].

Before you get too excited, though, this will not work on any interval. We don’t get \displaystyle\int_0^{\pi/4} \sin^2(x)\ dx = \dfrac{1}{2}(\pi/4). Generally speaking, you want the interval to consist of integer multiples of \pi/2.

Is that it?

Not quite. Roger Nelsen, in a paper entitled Symmetry and Integration described the following Putnam problem:

\displaystyle\int_0^{\pi/2} \dfrac{dx}{1 + \tan(x)^{\sqrt{2}}}

This problem is absolutely ridiculous. Wait—did I say ridiculous? I meant ridiculously easy!!! Consider the graph of \dfrac{1}{1 + \tan(x)^{\sqrt{2}}}:

It appears to have the same sort of symmetry as before. In fact, if we draw in few lines and do some shading, we get:

With just a modicum of thought, we see that \displaystyle\int_0^{\pi/2} \dfrac{dx}{1 + \tan(x)^{\sqrt{2}}} = \dfrac{1}{2}\left(\dfrac{\pi}{2}\right) = \dfrac{\pi}{4}.

Whoa! What is going on here?

Actually, a lot. But let me keep it simple (there are nice generalizations of what I’ll write here); I’ll give a heuristic argument for why these things work. The key is that the functions we’ve been dealing with are symmetric about a point. Without going into too much detail, let’s just say that a function f(x) is symmetric about a point (a, f(a)), which is the midpoint of an interval (c,d), if for any x such that a+x is still in the interval (c,d), the average of f(a+x) and f(a-x) is f(a), i.e., \dfrac{f(a+x) + f(a-x)}{2} = f(a). Truly, then, the average value of the function on (c,d) is f(a). However, we also know that the average value of any continuous function on an interval (c,d) is given by \dfrac{1}{d-c}\displaystyle\int_c^d f(x)\ dx. Therefore, f(a) = \dfrac{1}{d-c}\displaystyle\int_c^d f(x)\ dx or, equivalently, \displaystyle\int_c^d f(x)\ dx = (d-c)f(a).

In our case, (c,d) = (0, \pi/2), a = \pi/4, f(x) = \dfrac{1}{1 + \tan(x)^{\sqrt{2}}} and we get \displaystyle\int_0^{\pi/2} \dfrac{dx}{1 + \tan(x)^{\sqrt{2}}} =(\pi/2 - 0)\dfrac{1}{1 + \tan\left(\dfrac{\pi}{4}\right)^{\sqrt{2}}} = \dfrac{\pi}{4}. Well, except for one thing. We still need to show the averaging property. This is just a little bit of algebra, thankfully. First, I leave it as an exercise to show that \tan\left(\dfrac{\pi}{4} + x\right) = \dfrac{1}{\tan\left(\dfrac{\pi}{4} - x\right)} (try converting things into sines and cosines and using the angle addition formulas). Now, for simplicity, we write t = \tan\left(\dfrac{\pi}{4} + x\right). The average is now given by

\dfrac{1}{2}\left(\dfrac{1}{1+t^{\sqrt{2}}} + \dfrac{1}{1 + t^{-\sqrt{2}}}\right), where the negative exponent comes from \dfrac{1}{\tan\left(\dfrac{\pi}{4} - x\right)} = \dfrac{1}{t}.

Using our fraction addition trick, this becomes {\dfrac{1}{2}\left(\dfrac{2 + t^{-\sqrt{2}} + t^{\sqrt{2}}}{2 + t^{-\sqrt{2}} + t^{\sqrt{2}}}\right) = \dfrac{1}{2}} which is the required value.

“But perhaps, you shall not find her common, now”.

Posted by

11

This is the second in my series on techniques I use in the classroom. Many of the things I talk about in this series are well-known, in the sense that at least 50 people know about them. What is certain is that they are not well-known to students. This entry concerns something that I want my college students to have down pat, but on which I expect them to do rather poorly: adding and subtracting fractions.

Tricks of the Trade

(with Professor Glesser)

For simplicity, let me break up addition of fractions into three categories:

  1. Common Denominators
  2. One denominator is a multiple of the other
  3. Other (the algebraist in me wants to write, “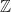\mathbb{Z}-linearly independent denominators”.)

Now, once you get by students wanting to do things like:

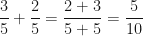\dfrac{3}{5} + \dfrac{2}{5} = \dfrac{2+3}{5+5} = \dfrac{5}{10} (batting average addition)

then students catch on pretty quickly that the common denominator case is where they want to be.  The second category of problems, exemplified here by

\dfrac{3}{5} - \dfrac{1}{10}

is only slightly more tricky. Any student who has ever needed to make change can figure out why you should think of \dfrac{3}{5} as \dfrac{6}{10}. In any case, I am going to assume that the students in question have mastered categories 1 and 2 (both in recognizing and computing).

Let’s up the ante a bit and try a problem like:

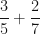
\dfrac{3}{5} + \dfrac{2}{7}

I was taught to find common denominators, i.e., find a common multiple of 5 and 7 and multiply each by an appropriate factor to get two fractions with common denominators. Here for instance, we note that the least common multiple of 5 and 7 is 35. Multiplying as follows:

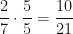
\dfrac{3}{5} \cdot \dfrac{7}{7} = \dfrac{21}{35} and \dfrac{2}{7}\cdot \dfrac{5}{5} = \dfrac{10}{21}

we get the new (easier) problem 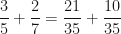\dfrac{3}{5} + \dfrac{2}{7} = \dfrac{21}{35} + \dfrac{10}{35} and we all know that the answer is 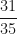\dfrac{31}{35}. No problem, right? Well, wrong. Students routinely mess this up. First, students are usually to taught to find the least common denominator and this, for many of them, is guess-work. Second, they tend to multiply fractions incorrectly in a way they never do for category 2 problems. Third, it is just too many steps for most of them to remember and/or complete without arithmetic errors. Heck, I even messed up the above problem when I typed it up the first time.

How the Pros Do It

Let’s take a more general situation: \dfrac{a}{b} + \dfrac{c}{d}. We can always find a common denominator by multiplying the denominators¹. So, we get \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{a}{b}\cdot \dfrac{d}{d} + \dfrac{c}{d}\cdot\dfrac{b}{b} = \dfrac{ad + bc}{bd}. Simply put, starting from the original problem, you cross multiply and add to get the numerator and multiply across to get the denominator.

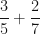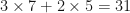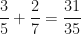
For example, \dfrac{3}{5} + \dfrac{2}{7} becomes easy now as the numerator is just 3 \times 7 + 2 \times 5 = 31 and the denominator is 5 \times 7 = 35, so \dfrac{3}{5} + \dfrac{2}{7} = \dfrac{31}{35}

Pictorially, it looks like: Teach your students this and it will amaze you how you no longer have to interrupt the flow of a demonstration to add fractions. Show them how useful it is in the kitchen when they need to know that \dfrac{1}{2} + \dfrac{1}{3} = \dfrac{5}{6} without the benefit of pencil and paper.

What about subtraction?

No problem! A similar derivation shows that to subtract, you simply cross multiply and subtract to get the numerator and multiply to get the denominator. For example, \dfrac{4}{9} - \dfrac{2}{5} = \dfrac{4 \times 5 - 2 \times 9}{9 \times 5} = \dfrac{2}{45}

The biggest problem students face when doing subtraction is remembering which order you subtract (it didn’t matter for addition!) If you always start with the down-right arrow, there is no issue, though. It’s amazing. I’ve taught this to students who could hardly subtract fractions on paper, but after learning this trick, would do the problems in their head as fast as I can.

What about algebra?

It is really convenient with many algebra problems. For instance, 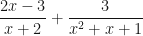\dfrac{2x - 3}{x+2} + \dfrac{3}{x^2 + x + 1} gives a lot of students fits as they can’t see how to find a common denominator. But, using this method:

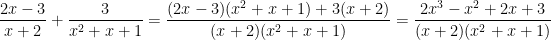{\dfrac{2x - 3}{x+2} + \dfrac{3}{x^2 + x + 1} = \dfrac{(2x-3)(x^2 + x + 1) + 3(x+2)}{(x+2)(x^2 + x + 1)}= \dfrac{2x^3 - x^2 + 2x + 3}{(x+2)(x^2 + x + 1)}}.

To be sure, the arithmetic is still hairy, but there is less writing than before and the student doesn’t have to think about this part, they can just do it. Now there are some cases where this method will result in some cancelling work. For example:

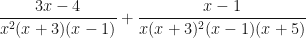\dfrac{3x - 4}{x^2(x+3)(x-1)} + \dfrac{x-1}{x(x+3)^2(x-1)(x+5)}.

A student should learn to recognize that it is much easier to multiply the first fraction by \dfrac{(x+3)(x+5)}{(x+3)(x+5)} and the second by \dfrac{x}{x} and then adding. But, if they are just getting started, as long as they aren’t too overzealous about distributing, they will obtain using this method

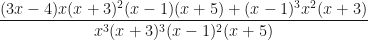
\dfrac{(3x-4)x(x+3)^2(x-1)(x+5) + (x-1)^3x^2(x+3)}{x^3(x+3)^3(x-1)^2(x+5)}

and the cancellation is not too hard to find, leaving 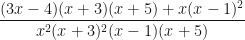\dfrac{(3x-4)(x+3)(x+5) + x(x-1)^2}{x^2(x+3)^2(x-1)(x+5)}.

Is it really a trick?

No, not really. The formula {\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad + bc}{bd}} actually defines fraction addition. In fact, if you’re interested in a little abstract algebra, hold on to your hats.

For the advanced reader who isn’t afraid of a little jargon

There is a lovely theorem in algebra saying that every integral domain can be embedded in a field. Huh? You ate what now?

All right, let’s break it down.

AG: An integral domain is just a commutative ring where…

Poor Reader: Whoa whoa whoa. Hold on just a second, there, professor. A what?

AG: Ah, yes, a commutative ring. It is a ring that is commutative.

PR: (eyes rolling) Yes, brilliant. What the heck is a ring? (looks nervously at his or her wedding band)

AG: It is an abstract structure composed of a non-empty set and two binary operations…um, long story short, it is a set where you can add and multiply and the distributive laws hold. The only real caveat is that sometimes multiplication isn’t commutative. That means that sometimes 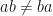ab \neq ba. Matrix multiplication is like this. In fact, the set of n \times n matrices forms a ring since you can add and multiply them as usual.

PR: Riiiigggghhttt (eyes are glazed over).

AG: A commutative ring is where you don’t have the multiplication problem. Then everything works just the way you want it to.

PR: Okay, let’s say for a moment I understand what you’re talking about. What is this integral domain thing then?

AG: Good question. Remember how you solve x^2 + 3x + 2 = 0? You factor to get (x+2)(x+1) = 0 and then conclude that x = -2 or x = -1. How do you conclude that?

PR: Well, we know that if 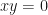xy = 0 then x = 0 or y = 0.

AG: Precisely. Any commutative ring that has that property, we call an integral domain.

PR: That is a stupid name. I think I could do better.

AG: Yes, yes, you’re very smart; now, shut up! The theorem is that every integral domain can be embedded in a field. A field is just an integral domain where you can divide by anything other than 0 (Even in abstract algebra, except in 1 case, we are never, ever, allowed to divide by 0).

PR: What do you mean by embedded?

AG: It is a bit technical. Strictly speaking, it means that there is an injective ring homomorphism from the integral domain into a field. But just think about how every integer is also a rational number.

PR: Rational number?

AG: I’m sorry: a fraction. See if I have the integer 4, I can think of it as \dfrac{4}{1} and then it is a fraction. This is how we embed the integers into the rational numbers, which are a field since you can divide by fractions.

PR: You can divide by integers too. Aren’t they a field?

AG: No, because if you divide by an integer, you don’t normally get an integer. Fields have to be closed. By that, I mean that when you divide, the answer is still in the field.

PR: Hmmm. I don’t think I understand this.

AG: That’s okay. If you could really learn it in a blog post, you wouldn’t have to take an entire year of it in graduate school. The point of all this is to get at the following. To build a field from an integral domain, you take the elements of the integral domain and start writing down all fractions from those elements. You need to then explain how to add and multiply those fractions.² The answer is to define these as

{\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad + bc}{bd}} and \dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd},

which is precisely how you do it normally. Now, there is a lot more to proving the theorem. There are issues of showing this is well-defined, that the usual laws of arithmetic (e.g., associativity, commutativity, distributivity) hold and that you can produce an injective ring homomorphism. This shows though, that it is not just more computationally efficient to add this way, but that when we don’t show it, we are actually missing out on a core ingredient of a key theorem in abstract algebra.

PR: (snoring)…hmm, what, oh yes, that is a shame. Did you check your pocket for the key?

________________________________________________________________________________

¹ This will likely not give you the least common denominator, but the only cost is that you’ll have to do some cancellation at the end.

² You also need to define when two fractions are the same: \dfrac{a}{b} = \dfrac{c}{d} if and only if ad = bc.